Procrustes superimposition

Authors
Affiliation

Floriane Remy

CNRS, Univ. Bordeaux, MCC – UMR 5199 PACEA

Frédéric Santos

CNRS, Univ. Bordeaux, MCC – UMR 5199 PACEA

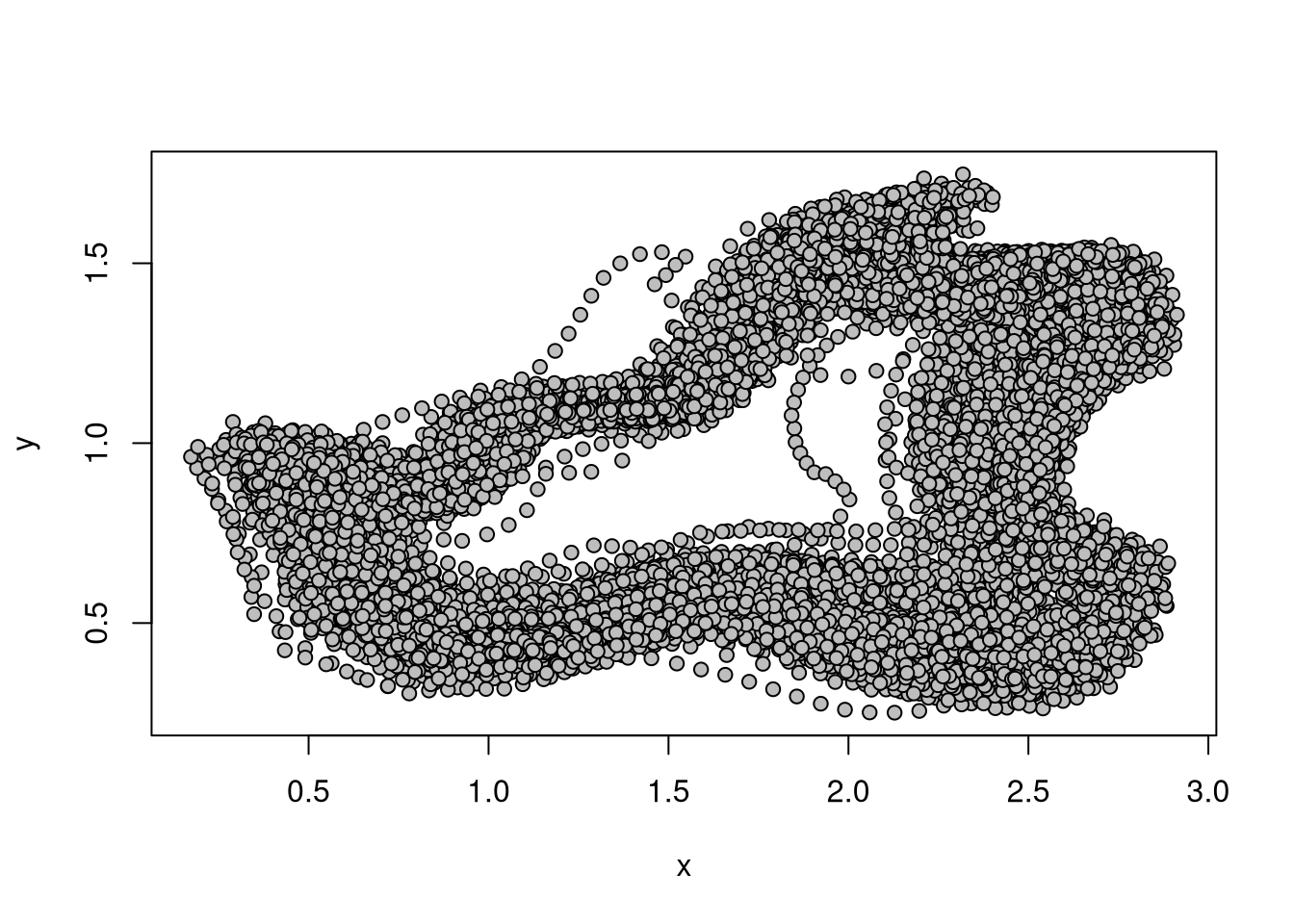
Generally speaking, geometric morphometric studies are often based on the analysis of Procrustes coordinates, generated from the superimposition of the individuals, after a translation, rotation and scaling (Rohlf 1999; Ross 2004).

1 Procrustes analysis with R

In R, you have several options to perform a procrustes analysis on a landmarks configuration:

  • the function geomorph::gpagen();
  • the function Morpho::procSym();
  • the function shapes::procGPA();
  • and probably many others.

In all cases, your landmark data must be stored in an array.

You can perform either a complete procrustes analysis (in this case, all individuals are scaled at the same unit centroid size), or a partial procrustes analysis (in this case, size differences are not removed), depending on the aim of your study.

Figure 1 presents the landmarks of all specimens before the procrustes superimposition.

geomorph::plotAllSpecimens(rats, mean = FALSE)
Figure 1: Plot of all landmark configurations, in the original coordinate system.

Note that this step should not be skipped in practice. Indeed, before beginning the analyses, it is best to make sure that there are no trivial errors in the data: did we make any mistake in the ordering of our landmarks (impairing the condition of landmarks homology)? Is there any landmark with a huge variation among specimens? Is an obvious problem with some given specimen? Figure 1 allows for simple checks to avoid common errors.

Exercise

Perform a (complete) procrustes analysis on the R object rats previously created.

If needed, you can read the help pages of the corresponding R functions; for instance with help(gpagen). Pay extra attention to the argument curves, which indicates how to define sliding semi-landmarks along curves.

## Perform a GPA with geomorph:
gpa <- geomorph::gpagen(
  A = rats,
  curves = define.sliders(landmarks = c(1, 16:103, 1))
)

Note that if you are using semilandmarks, you can make them slide taking in consideration the bending energy with gpagen().

  • For curve sliding semilandmarks: the argument curves may be defined using define.sliders() to specify the indices of the semilandmarks to be slided.
  • For surface sliding semilandmarks: the argument surfaces should specify the indices of the semilandmarks to be slided.

2 Visualize the results

You can get of a summary of the results of the superimposition with:

summary(gpa)

Call:
geomorph::gpagen(A = rats, curves = define.sliders(landmarks = c(1,  
    16:103, 1))) 



Generalized Procrustes Analysis
with Partial Procrustes Superimposition

15 fixed landmarks
88 semilandmarks (sliders)
2-dimensional landmarks
11 GPA iterations to converge
Minimized Bending Energy used


Consensus (mean) Configuration

                X             Y
1   -0.1453336845  0.0348523448
2   -0.1062902004  0.0117796511
3   -0.0737512382  0.0295356044
4   -0.0402893300  0.0289108226
5   -0.0186376605  0.0261633920
6    0.0704159222  0.0712798868
7    0.0570564575  0.0497289658
8    0.1019204713  0.0466197618
9    0.1206741051  0.0196550432
10   0.0834215402 -0.0192995978
11   0.1090629837 -0.0536144540
12  -0.0154259068 -0.0399086907
13  -0.0668048461 -0.0417049048
14  -0.1012721966 -0.0381679364
15  -0.1332119827 -0.0121211859
16  -0.1390495240  0.0340554449
17  -0.1337909522  0.0304940044
18  -0.1286865976  0.0250230663
19  -0.1220359741  0.0195539556
20  -0.1144811400  0.0146696752
21  -0.0976006317  0.0118251796
22  -0.0898651536  0.0145403402
23  -0.0833677503  0.0191090686
24  -0.0784169858  0.0244613538
25  -0.0670183119  0.0302747043
26  -0.0604879631  0.0304631589
27  -0.0538447560  0.0302351433
28  -0.0471369415  0.0295661412
29  -0.0327517978  0.0275828119
30  -0.0255092694  0.0266720028
31  -0.0090616626  0.0278924847
32  -0.0001200072  0.0319699592
33   0.0083528155  0.0375514074
34   0.0166708769  0.0438255554
35   0.0249810681  0.0503332192
36   0.0334315143  0.0567544699
37   0.0422126068  0.0628088020
38   0.0515405756  0.0679917597
39   0.0612111185  0.0713930934
40   0.0660847179  0.0676383547
41   0.0597297938  0.0591492875
42   0.0606250236  0.0454278859
43   0.0670126223  0.0427211756
44   0.0745839467  0.0421008275
45   0.0824230285  0.0426571804
46   0.0896127375  0.0442821627
47   0.0958995909  0.0460899613
48   0.1095143938  0.0473961786
49   0.1167283293  0.0463110741
50   0.1227363964  0.0425869630
51   0.1260244066  0.0363127849
52   0.1268548384  0.0288367055
53   0.1246608837  0.0225832678
54   0.1150330219  0.0179046183
55   0.1092791525  0.0150155760
56   0.1035196233  0.0110982408
57   0.0980711264  0.0062410828
58   0.0930809228  0.0007436957
59   0.0888148437 -0.0053808565
60   0.0854954053 -0.0120251366
61   0.0827932431 -0.0263221159
62   0.0840195681 -0.0330488131
63   0.0871851779 -0.0387723602
64   0.0924054861 -0.0423578253
65   0.0981849597 -0.0445243015
66   0.1036355643 -0.0464708839
67   0.1074392890 -0.0496150268
68   0.1049582375 -0.0603870874
69   0.0990452173 -0.0659589054
70   0.0913344036 -0.0696366480
71   0.0826809029 -0.0713612200
72   0.0735948865 -0.0712111458
73   0.0642870525 -0.0698363458
74   0.0549609162 -0.0676752539
75   0.0457168604 -0.0649546222
76   0.0366511606 -0.0617001884
77   0.0277653598 -0.0580514242
78   0.0190872417 -0.0540122195
79   0.0105558322 -0.0498610158
80   0.0020333691 -0.0458813533
81  -0.0066293393 -0.0424690276
82  -0.0228478034 -0.0391175376
83  -0.0300874900 -0.0390156915
84  -0.0374675417 -0.0393976319
85  -0.0449048630 -0.0400140574
86  -0.0523190996 -0.0406927196
87  -0.0596000814 -0.0413543288
88  -0.0740460470 -0.0404177341
89  -0.0809371974 -0.0389117126
90  -0.0876313250 -0.0381147674
91  -0.0944396502 -0.0381805641
92  -0.1081826911 -0.0346678327
93  -0.1145603746 -0.0301023975
94  -0.1206699153 -0.0252001584
95  -0.1266213471 -0.0204311466
96  -0.1319134150 -0.0159316693
97  -0.1323216506 -0.0058768768
98  -0.1342228762  0.0012851288
99  -0.1368763741  0.0084519813
100 -0.1395812892  0.0150013062
101 -0.1411420357  0.0214742383
102 -0.1419566674  0.0273101990
103 -0.1431717556  0.0319001435

Note that, in particular, this gives you the consensus (or mean shape) of all individuals.

For a more graphical output, you can use:

plot(gpa)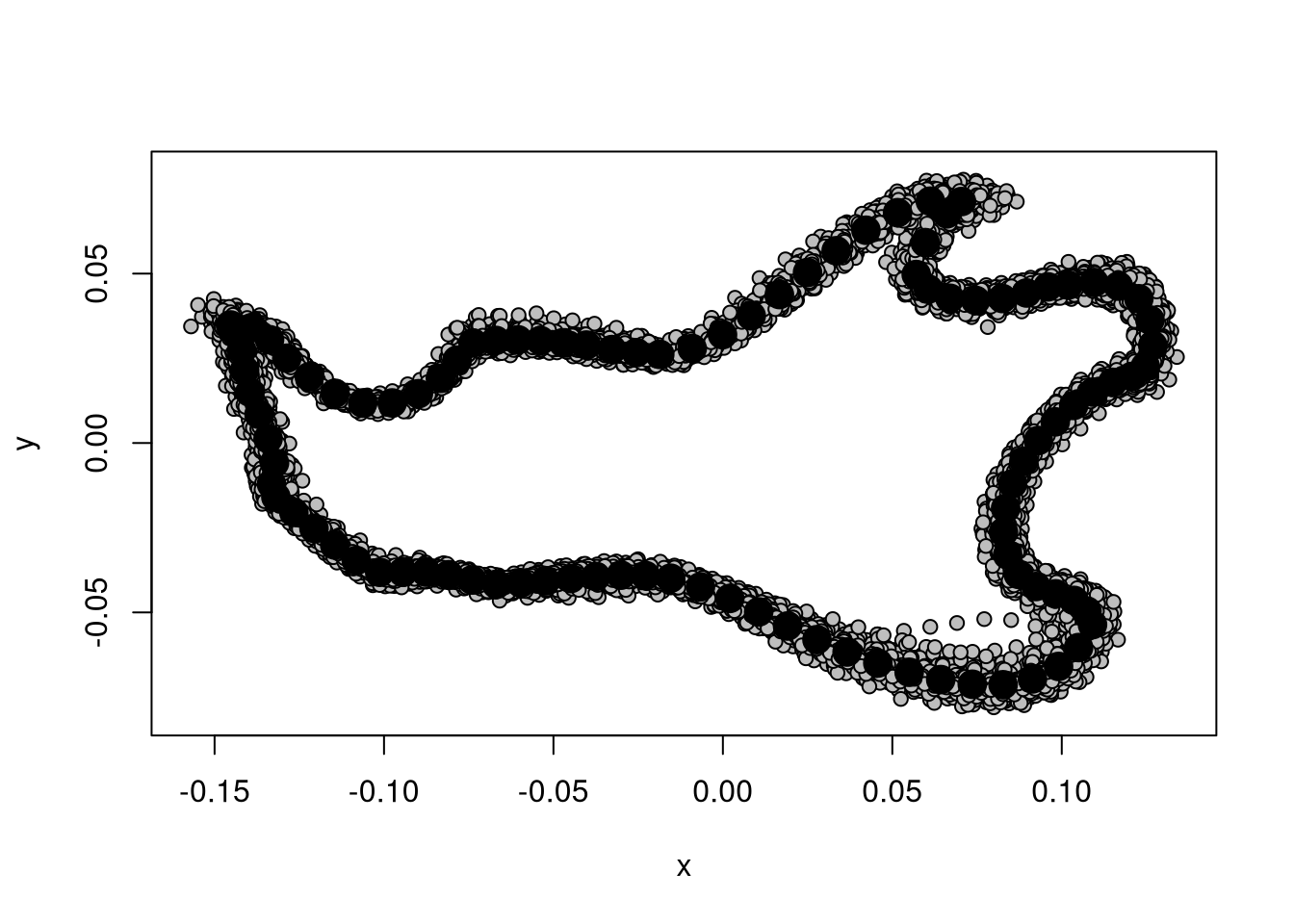
Figure 2: Mean shape and landmark configurations after procrustes superimposition.

You can compare this result to Figure 1.

Back to top

References

Rohlf, F. James. 1999. “Shape Statistics: Procrustes Superimpositions and Tangent Spaces.” Journal of Classification 16 (2): 197–223. https://doi.org/10.1007/s003579900054.
Ross, Amy. 2004. “Procrustes Analysis.”