Assessing the effect of covariates

Authors
Affiliation

Floriane Remy

CNRS, Univ. Bordeaux, MCC – UMR 5199 PACEA

Frédéric Santos

CNRS, Univ. Bordeaux, MCC – UMR 5199 PACEA

In this section, we will illustrate a possible approach to assess the effect of some covariates on the shape: sex, body mass, etc. We will see in the next section a specific discussion about the effect of size on shape, also called allometry.

Statistical tests in morphometrics

As a general advice, using permutation tests, or bootstrap procedures, rather than “classical” parametric tests is a good idea in morphometrics. For the rationale behind this fact, see for instance Webster and Sheets (2010).

Note that all functions for statistical inference included in {geomorph} use permutation or bootstrap tests. More generally, R packages such as {RRPP} or {vegan} implement such tests. For a very nice and friendly introduction to permutation tests and bootstrap, see for instance Zieffler, Harring, and Long (2011), Rousselet, Pernet, and Wilcox (2023) or Davison and Hinkley (1997).

Generally speaking, to assess the impact of a given covariate on shape (i.e., on Procrustes coordinates), we can for instance use:

1 Reshape data

If you want to stay within the {geomorph} framework, you can use the function geomorph::gm.data.frame() to store both the (aligned) coordinates and a set of covariates in a dataframe-like object1.

## Create a dataframe-like object for subsequent analyses with geomorph:
gm.dtf <- geomorph.data.frame(
  coords = gpa$coords,
  csize = gpa$Csize,
  weight = meta$Weight,
  sex = meta$Sex,
  age = meta$Age,
  age_class = meta$Age_class,
  season = meta$Season,
  location = meta$Location
)

If you want to be free from the {geomorph} framework and prefer handling more general and standard R objects (so that you can use them with any other R package of your choice), this code block provides an alternative:

## Create a dataframe-like object for subsequent analyses with geomorph:
gen.dtf <- data.frame(
  two.d.array(gpa$coord),
  csize = gpa$Csize,
  weight = meta$Weight,
  sex = meta$Sex,
  age_class = meta$Age_class,
  season = meta$Season,
  location = meta$Location
)

2 Sexual dimorphism

First, let’s begin by studying the influence of sex on shape2.

2.1 PCA revisited

We can generate our PCA plots once again, but this time, introduce a different color for points according to the sex of the individuals. Below, the argument col allows for coloring the points according to a given factor.

## PCA with geomorph:
plot(gm.prcomp(gm.dtf$coords), pch = 16, col = gm.dtf$sex)
legend("topright", pch = 16, col = 1:2,
       legend = c("F", "M"))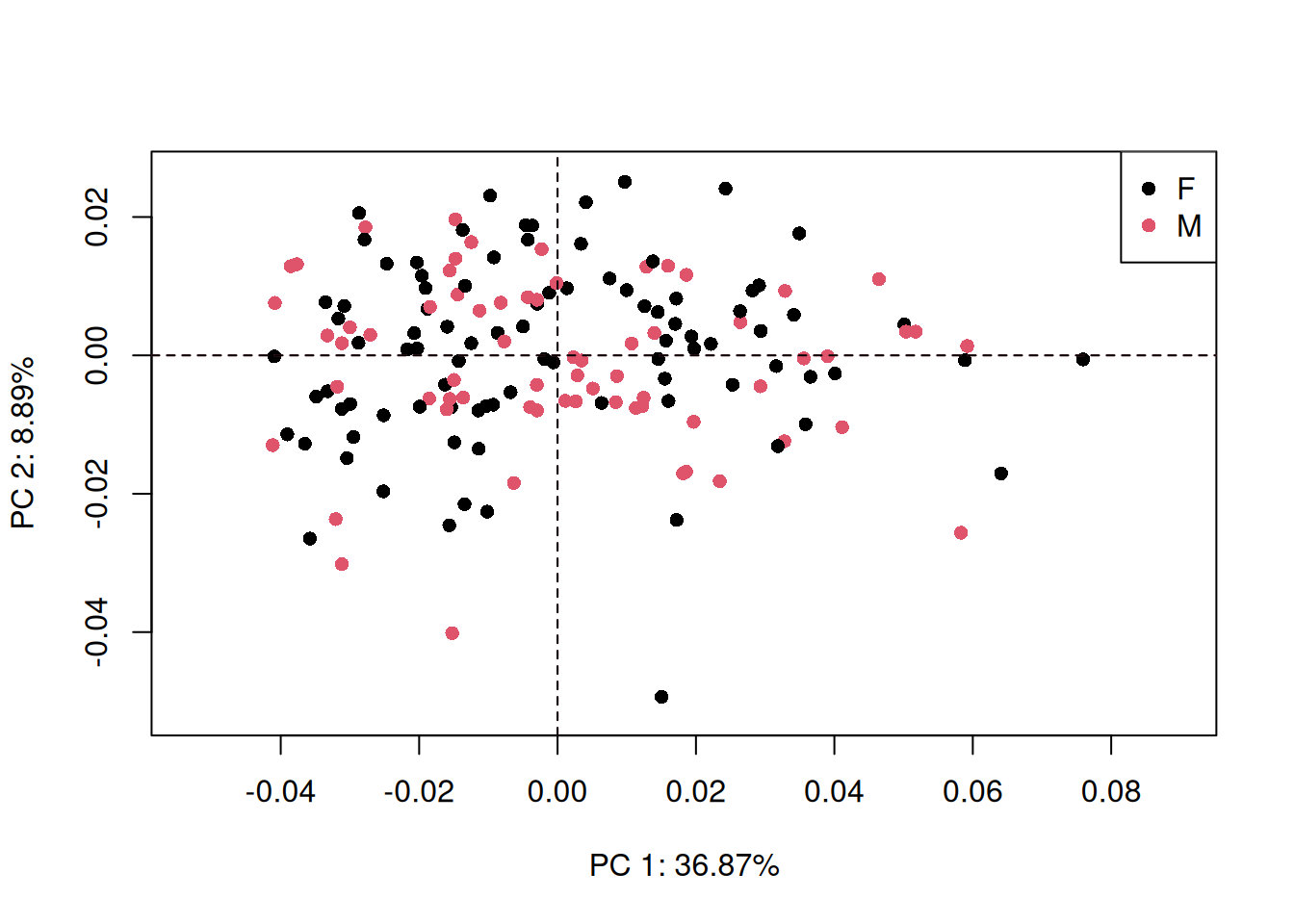
Figure 1: PCA of the shape variation according to sex (female or male). PCA produced with {geomorph}.

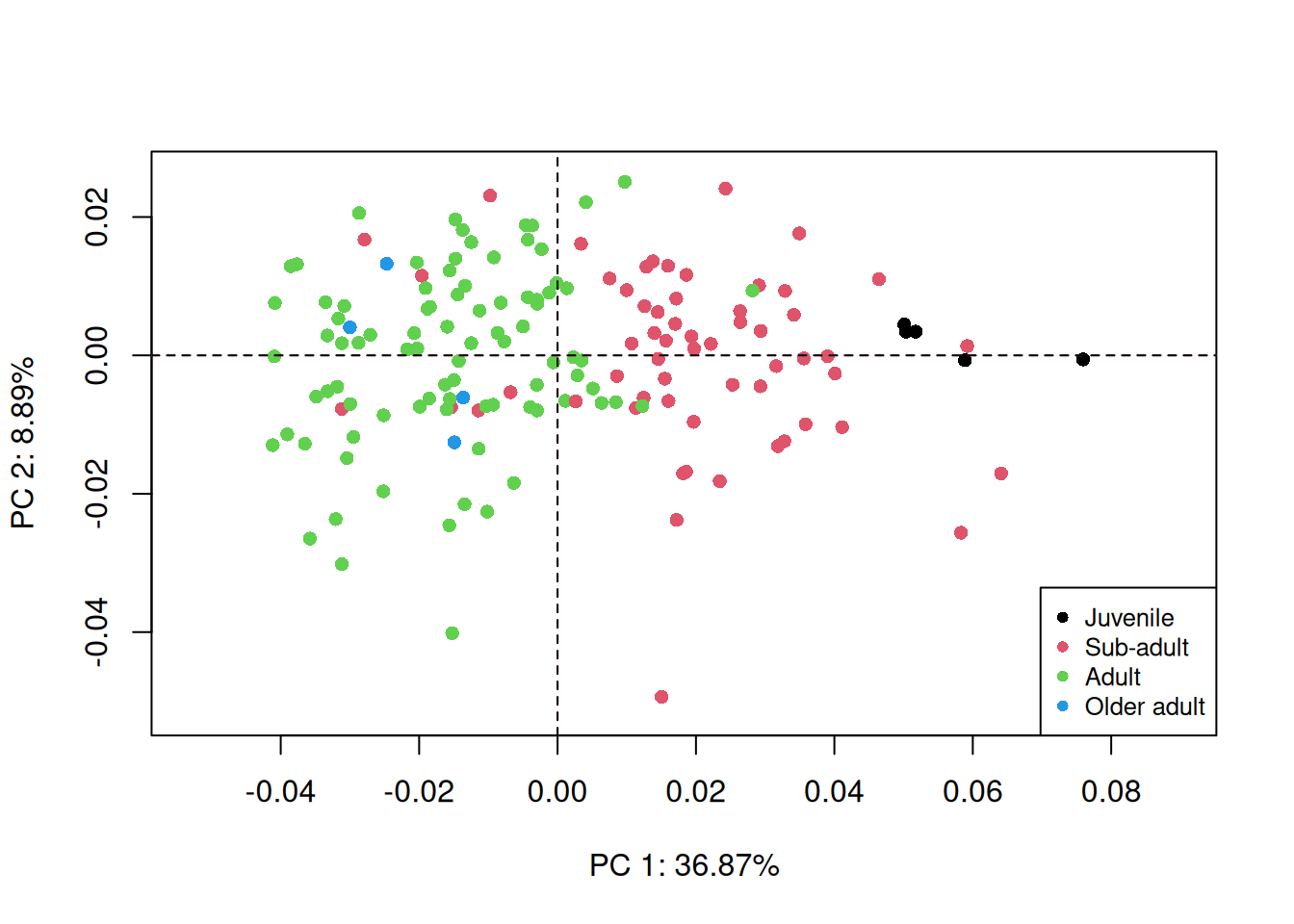
How would you interpret Figure 1?

2.2 Statistical inference

To test formally the influence of sex on shape, one can use an analysis of variance of the Procrustes coordinates (or, maybe, on the coordinates of individuals on the first principal axes of the PCA, which is also a perfectly valid approach). For that, you may want to use the function geomorph::procD.lm()3:

## Analysis of variance:
procD.lm(coords ~ sex, data = gm.dtf, print.progress = FALSE) |>
  summary()

Analysis of Variance, using Residual Randomization
Permutation procedure: Randomization of null model residuals 
Number of permutations: 1000 
Estimation method: Ordinary Least Squares 
Sums of Squares and Cross-products: Type I 
Effect sizes (Z) based on F distributions

           Df       SS        MS   Rsq      F       Z Pr(>F)
sex         1 0.001649 0.0016493 0.006 0.9477 0.29544  0.383
Residuals 157 0.273228 0.0017403 0.994                      
Total     158 0.274877                                      

Call: procD.lm(f1 = coords ~ sex, data = gm.dtf, print.progress = FALSE)

An alternative is the function Morpho::permudist():

permudist(pca$x, groups = gm.dtf$sex, rounds = 1000)$p.value
          F
M 0.5564436
Exercise

In the light of all previous results, what can you say about the amount of sexual dimorphism in the dataset?

3 Other qualitative covariates

Exercise
  1. Follow the same approach as in the previous section to assess the impact of age classes on the shape. We will see more elements to discuss these results in the next section.
  2. Same question for the other qualitative covariates: season, location.

For a PCA illustrating age classes:

## PCA plot with age classes:
plot(gm.prcomp(gm.dtf$coords), pch = 16, col = gm.dtf$age_class)
legend("bottomright", pch = 16, col = 1:4, cex = 0.8,
       legend = levels(gm.dtf$age_class))
Figure 2: PCA of the shape variation according to age classes. PCA produced with {geomorph}.

An alternative with {factoextra} instead, for a fancier plot:

## PCA with age classes (a bit fancier):
pca.age <- gen.dtf |>
  subset(! is.na(age_class)) |>
  PCA(quanti.sup = 207:208, quali.sup = 209:212,
           scale.unit = FALSE, graph = FALSE)
fviz_pca_ind(pca.age, habillage = 210, geom = "point",
             legend.title = "Age classes") +
  stat_chull(aes(fill = age_class), geom = "polygon", alpha = 0.1)
Figure 3: PCA of the shape variation according to age classes PCA produced with {factoextra}.

4 Other quantitative covariates

We can also evaluate the potential effect of quantitative variables, such as age (in days), weight, etc. For the study and assessment of the relation between the shape and these quantitative covariates, regression analyses may be useful.

For instance, to study the influence of weight (in grams):

## Regression of weight on shape:
reg.weight <- procD.lm(
  coords ~ weight,
  data = gm.dtf,
  print.progress = FALSE
)
reg.weight$aov.table
           Df       SS       MS     Rsq      F      Z Pr(>F)    
weight      1 0.061471 0.061471 0.22363 45.224 4.6768  0.001 ***
Residuals 157 0.213406 0.001359 0.77637                         
Total     158 0.274877                                          
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Another (simpler) approach might be to represent a scatterplot of weight and the first two axes of the PCA:

par(mfrow = c(1, 2))
plot(pca$x[, 1] ~ gen.dtf$weight, pch = 16,
     xlab = "Weight", ylab = "PC 1")
plot(pca$x[, 2] ~ gen.dtf$weight, pch = 16,
     xlab = "Weight", ylab = "PC 2")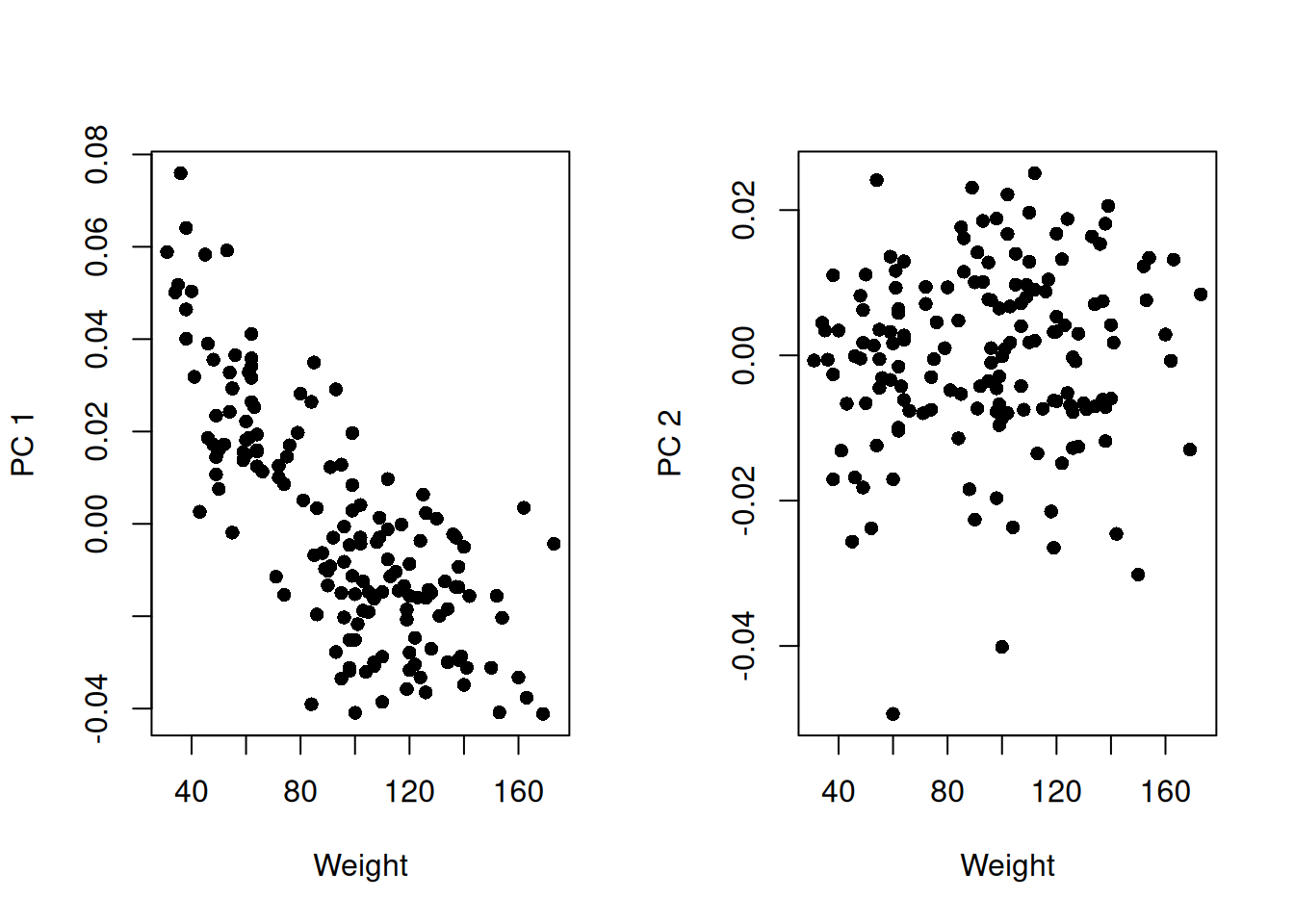
Figure 4: Scatterplots for the relation between weight and the shape principal axes.
Exercise
  1. Based on the results of the regression analyses, what are your conclusions regarding the potential effect of weigth on shape variation of the mandible?
  2. Same question regarding body length.
  3. Same question about tail length.

5 Covariation, integration

Finally, it could be interesting in some cases to investigate the covariation between different anatomical units (e.g., mandible and skull base – this is called integration and modularity, see Klingenberg works for more information on this topic), or between an anatomical structure and quantitative covariate. In pratcise, these questions of covariation can often be investigated with a method called Partial Least Square analyses. See Butaric and Maddux (2016), Neaux (2017), Zlolniski et al. (2019), or Pitirri and Begun (2020) for nice examples of use of this method in biological anthropology.

Back to top

References

Butaric, Lauren N., and Scott D. Maddux. 2016. “Morphological Covariation Between the Maxillary Sinus and Midfacial Skeleton Among Sub-Saharan and Circumpolar Modern Humans: Maxillary Sinus Shape in Humans.” American Journal of Physical Anthropology 160 (3): 483–97. https://doi.org/10.1002/ajpa.22986.
Davison, A. C., and D. V. Hinkley. 1997. Bootstrap Methods and Their Application. Cambridge ; New York, NY, USA: Cambridge University Press.
Neaux, Dimitri. 2017. “Morphological Integration of the Cranium in Homo, Pan, and Hylobates and the Evolution of Hominoid Facial Structures.” American Journal of Physical Anthropology 162 (4): 732–46. https://doi.org/10.1002/ajpa.23163.
Pitirri, M. K., and David Begun. 2020. “Ontogenetic Insights into the Significance of Mandibular Corpus Shape Variation in Hominoids: Developmental Covariation Between M2 Crypt Formation and Corpus Shape.” American Journal of Physical Anthropology 171 (1): 76–88. https://doi.org/10.1002/ajpa.23969.
Rousselet, Guillaume, Cyril R. Pernet, and Rand R. Wilcox. 2023. “An Introduction to the Bootstrap: A Versatile Method to Make Inferences by Using Data-Driven Simulations.” Meta-Psychology 7. https://doi.org/10.15626/MP.2019.2058.
Webster, Mark, and H. David Sheets. 2010. “A Practical Introduction to Landmark-Based Geometric Morphometrics.” The Paleontological Society Papers 16: 163–88. https://doi.org/10.1017/S1089332600001868.
Zieffler, Andrew, Jeffrey Harring, and Jeffrey D. Long. 2011. Comparing Groups: Randomization and Bootstrap Methods Using R. Hoboken, N.J: Wiley.
Zlolniski, Stephanie Lois, Nicole Torres-Tamayo, Daniel García-Martínez, Esther Blanco-Pérez, Federico Mata-Escolano, Alon Barash, Shahed Nalla, Sandra Martelli, Juan A. Sanchis-Gimeno, and Markus Bastir. 2019. “3D Geometric Morphometric Analysis of Variation in the Human Lumbar Spine.” American Journal of Physical Anthropology 170 (3): 361–72. https://doi.org/10.1002/ajpa.23918.

Footnotes

  1. Formally, this is not really a dataframe, but the data created or reshaped using this function will behave as a dataframe for all functions from the {geomorph} package. Note that this kind of object will not make sense outside of the {geomorph} world in R.↩︎

  2. In a real study, this would probably require to control for the effect of age at the same time, or to study adults only. But one problem at a time!↩︎

  3. Formally, this function is only a wrapper for the function RRPP::lm.rrpp(), that we shall use later on.↩︎